Ohyb elektromagnetického záření
Physical Background
Ohybové jevy, které vznikají v těsné blízkosti překážky při průchodu světla z bodového zdroje podrobně zkoumal Fresnel. Při těchto jevech, které nazýváme Fresnelovy ohybové jevy, jde o problém řešení interference kulových vln na základě Huygensova principu. Pokud však uvažujeme ohyb světla z dost vzdáleného zdroje (monochromatického koherentního záření), vlnoplocha je prakticky už rovinná. Tím se dostáváme k jevům, které vznikají při ohybu svazku rovnoběžných paprsků s přesně rovinnými vlnoplochami, a které se nazývají Fraunhoferovy ohybové jevy.
Pokud jsme v experimentu v dostatečné vzdálenosti od zdroje kvalitativní i kvantitativní analýzu nám vysvětlí Fraunhoferův ohybový jev – v našem případě na jednorozměrné štěrbině. Štěrbina AC šířky d osvětlená kolmo dopadajícím monochromatickým světlem (jednobarevným světlem, t.j. světlem s jednou vlnovou délkou) se stává v každém svém bodě v celé své šířce zdrojem elementárních vln (podobně jako rozhraní mezi dvěma prostředími při lomu a odrazu). Ze všech bodů se šíří kulové vlnoplochy. Protože však paprsky vystupují všemi směry interferují mezi sebou,a světlo se za štěrbinou nešíří rovnoměrně na všechny strany, jak pozorované rozdělení intenzity v experimentu ukazuje.
Vyberme si ze všech paprsků rovnoběžný svazek paprsků vystupujících ze štěrbiny pod úhlem α (odklon od původního směru paprsků před dopadem na štěrbinu, viz obr. 1).
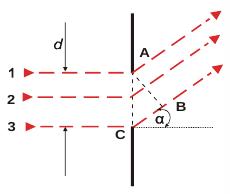
Obr. 1 K teorii Fraunhoferova ohybového jevu na štěrbině
V rovinné vlnoploše AB, kolmé na směr šíření vlnění, mají jednotlivé svazky různou fázi, podle délky uražené dráhy. Pokud je např. δ zpoždění krajního paprsku CB vzhledem k druhému krajnímu paprsku v bodě A (paprsek 1), je zpoždění paprsku, který prochází středem štěrbiny (t.j. osového paprsku) poloviční, teda δ/2. Fázový rozdíl všech ostatních paprsků roste úměrně se vzdáleností paprsků od bodu A k bodu C. Pak ke každému paprsku p (nacházejícímu se mezi paprsky 1 a 2) najdeme mezi paprsky 2 a 3 takový paprsek p´, který bude vzdálený o půl šířky štěrbiny) a jeho dráhový rozdíl bude δ/2. Z toho můžeme usuzovat, že všechny paprsky se budou rušit pokud, jejich zpoždění je rovné nepárovému počtu polovln, tedy pokud bude odchylka paprsků taková, že se δ rovná párovému počtu polovln a teda celočíselnému násobku vln, což vyjadřuje rovnice:
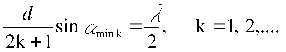
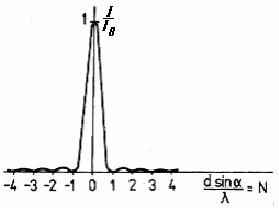
Obr. 2 Rozložení intenzity záření po průchodu štěrbinou šířky d
Vysvětlení ohybového jevu pro potřeby laboratorní úlohy provedeme jen na základě elementárních představ z obr. 1 a použijeme teorii, ve které se předpokládá, že dopadající vlna na štěrbinu je rovinná (obr. 1), t.j. jedná se o Fraunhoferův ohybový jev.
Předpokládejme, že rovinná monochromatická a koherentní vlna dopadá na jedinou štěrbinu šířky d = |AC| a odchyluje (ohýbá) se od původního směru o úhel α definující náhodně vybraný směr (viz obr. 1). Pokud by se vzdálenost |BC| rovnala právě vlnové délceλ, potom můžeme z úsudku snadno zjistit, že součet intenzit elektrického pole všech paprsků (elektromagnetického záření), které ze štěrbiny vystupují v tomto směru, je nulový, jinými slovy se tyto paprsky navzájem vyruší. Ke každému paprsku mezi paprsky 1 a 2 připadá totiž paprsek z druhé poloviny štěrbiny 2 až 3, který se od něho liší právě o dráhový rozdíl λ/2, takže se s ním v důsledku interference ruší (takovou dvojici představují např. paprsky 1 a 2, přičemž paprsky 1 a 3 jsou limitně blízko k okraji štěrbiny a jeden z nich – nevykompenzovaný, nehraje žádnou roli). Proto, když zvážíme platnost vztahu |BC| = d.sin α a připustíme libovolný nenulový celočíselný násobek vlnové délky λ, dostaneme úvahou podmínku pro polohu minim (3). Exaktním řešením (např. [1]) ohybového jevu, které však není pro potřeby praktika nevyhnutné, Frauenhofer získal rozložení intenzity procházejícího záření s hlavním maximem a symetricky s vedlejšími maximy a minimy (obr. 2). Intenzitu záření po průchodu štěrbinou lze vyjádřit jako funkci úhlu α:

-
Poloha minim intenzity (t.j. I(α) / I(0) = 0 ) je ve směrech, kde je splněná podmínka:
resp. podmínka pro úhly αmin, pro které nastává minimum, je:
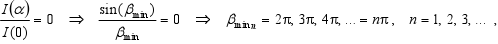
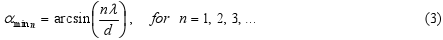
-
Poloha maxim intenzity (t.j. I(α)/I(0) = max.) je potom v místech, kde je splněná podmínka:
nebo podmínka pro úhly αmax, při kterých nastává maximum, je:
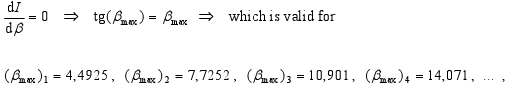
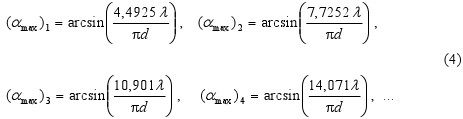
-
Relativní velikost maxim intenzity (t.j. I(α) / I(0) ) v místech, kde je splněná podmínka (4), je:
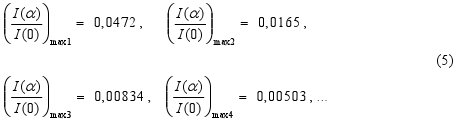
Autor studijního textu: Prof. Dr. František Schauer, Univerzita Tomáše Bati ve Zlíně
