Vlastní a vynucené oscilace
Physical Background
Harmonický oscilátor
Těleso vykonávající harmonický kmitavý pohyb nazýváme harmonický oscilátor. Může jím být například těleso na pružině (obr. 1), nebo atom či molekula pevné látky. Když při jeho pohybu zanedbáme odpor prostředí, hovoříme o netlumeném harmonickém oscilátoru. Můžeme ukázat, že kmitání je vždy harmonické, když je působící síla úměrná výchylce z rovnovážné polohy.
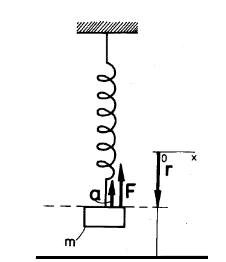
Obr. 1 Schematická reprezentace harmonického oscilátoru, F - elastická síla, r – výchylka, a - zrychlení
Máme pružinu, na jejíž prodloužení o r je potřebná síla F = -kr, kde k je tuhost pružiny. Pohybová rovnice harmonického oscilátoru, který je tvořen touto pružinou a závažím hmotnosti m, je (jako aplikace druhého Newtonova zákona ΣF = ma):


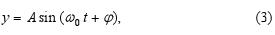
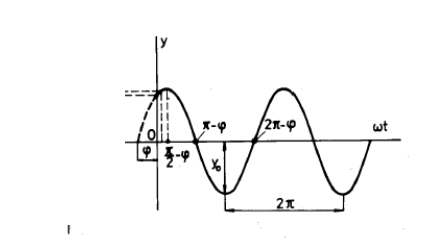
Obr. 2 Grafické vyjádření pohybu harmonického oscilátoru
Pro vlastní úhlovou rychlost harmonického oscilátoru můžeme napsat:
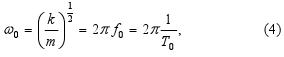
Tlumený oscilátor
Při pohybu harmonického oscilátoru v reálných podmínkách působí vždy třecí síly, které amplitudu kmitavého pohybu zmenšují a po určitém čase kmitání přestane. Takový oscilátor nazýváme tlumený oscilátor.
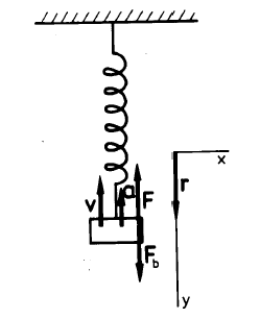
Obr. 3 Tlumený oscilátor a) F je elastická síla, Fb je brzdná síla, r je výchylka, v je okamžitá rychlost a a je okamžité zrychlení, b) s tlumením v důsledku tření v kapalině
Třecí síla je při malých rychlostech přímo úměrná okamžité rychlosti tělesa v hmotnosti m:
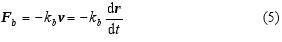

Zavedeme veličinu b = kb/(2m), která se nazývá konstanta útlumu, [b] = s−1. Pro malé tlumení (b < ωo) má rovnice (6) řešení, (když si uvědomíme, že podle obr. 3 platí r = jy):
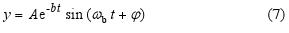
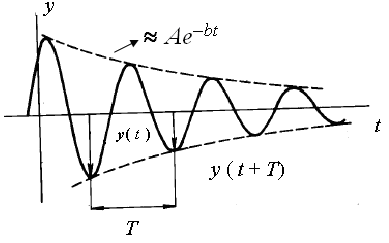
Obr. 4 Grafické vyjádření časové závislosti výchylky tlumeného oscilátoru
Nucené kmity oscilátoru
Významným případem kmitavého pohybu jsou takzvané nucené oscilace, při kterých vnější síla nutí látkový objekt kmitat s všeobecně jiným kmitočtem než je kmitočet vlastních kmitů. Když se však oba kmitočty k sobě přibližují, vzniká důležitý jev, který nazýváme rezonance. Předpokládejme, že na závaží z obr. 1 působí vynucující periodická sila:


Obr. 5 Tlumený oscilátor s působícími silami: Fv - vynucující síla, F - elastická sila, Fb - brzdná sila, r je okamžitá výchylka, v okamžitá rychlost a a je okamžité zrychlení tělesa hmotnosti m.
Když vezmeme v úvahu všechny síly, které způsobují pohyb závaží, můžeme napsat pohybovou rovnici pro pohyb v ose y:
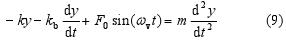
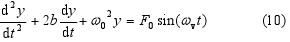


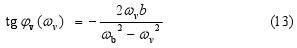
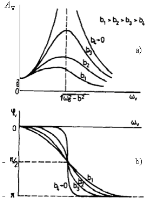
Obr. 6 Grafický průběh: a) amplitudy vynucených kmitů Av s koeficientem tlumení b jako parametr, b) fáze vynucených kmitů φv, v závislosti na úhlové frekvenci ωv vynucující síly
Z grafů na obr. 6 vyplývá mnoho zajímavých poznatků pro vynucený harmonický pohyb. Za prvé, je zřejmé, že amplituda vynucených kmitů Av (viz obr. 6 a) je funkcí úhlové frekvence ωv vynucující síly. Maximum amplitudy pro vynucený harmonický pohyb nastává pro takzvanou rezonanční frekvenci:

Závislosti na obr. 6 můžeme využít k určení přenosu energie na oscilátor. Tento proces je velmi důležitý v přírodě a všeobecně v technologiích, protože reprezentuje selektivní přenos energie mezi vysílačem energie a oscilátorem jen v určitých intervalech frekvencí, resp. vlnových délek. Tento jev tvoří např. základ selektivního přenosu telekomunikačních signálů, nebo absorbci určitých vlnových délek slunečního záření určitými molekulami, které, mimo jiného, dosáhnou povrchu Země.
Přenos energie za jednotku času na oscilátor (nebo okamžitý výkon Pv, který je funkcí času) z vynucujícího zdroje je:
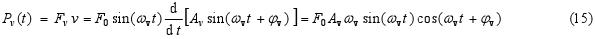
Střední hodnota energie přenesená za jednu periodu harmonického pohybu oscilátoru ze zdroje vynucující síly na oscilátor závisí na úhlové frekvenci vynucující síly ωv. Více informací můžete najít v práci R. B. Lindsay, Physical Mechanics, 3rd ed., Van Nostrand 1962).
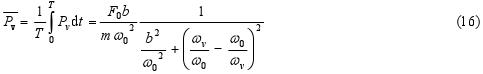
Obr. 7 prezentuje přenos střední hodnoty energie po dobu jedné periody harmonického pohybu na oscilátor ze zdroje vynucující síly jako funkci úhlové frekvence ωv, pro dvě různé hodnoty tlumení b.
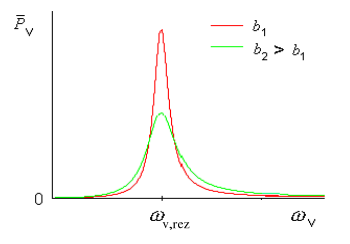
Obr. 7 Závislost přeneseného středního výkonu po dobu jedné periody pohybu harmonického oscilátoru (pro dvě různé hodnoty tlumení b).
Autor studijního textu: Prof. Dr. František Schauer, Univerzita Tomáše Bati ve Zlíně
