Vnější fotoefekt
Physical Background
Ke studium vnějšího fotoelektrického jevu si můžete vybrat jednu ze dvou standardních metod:
- Metoda nabíjení kondenzátoru na brzdné napětí – jednodušší metoda.
- Studium V-A charakteristiky vakuové fotonky – komplexnější metoda, vhodná pro studenty technických oborů a VŠ.
A. Metoda nabíjení kondenzátoru na brzdné napětí
V této úloze zkoumáme vlastnosti vnějšího fotoelektrického jevu metodou nabíjení kondenzátoru na tzv. brzdné napětí U0(f). Vnější fotoefekt, tedy vyražení, úplné uvolnění elektronu ven z fotokatody světlem, které na fotokatodu dopadá, nastává pouze v případě, že frekvence f dopadajícího světla je větší než tzv. mezní frekvence (též prahová frekvence) fm
| f > fm . | (3) |
Elektron vyražený z fotokatody doletí k anodě jen v případě, má-li k tomu dostatečnou kinetickou energii Ek,max. = mev2/2, neboť musí překonat odpudivé elektrické síly. Uvědomíme-li si, že elektrické napětí U odpovídá práci We elektrických sil potřebné na přenesení jednotkového elektrického náboje Q v elektrickém poli (U = We/Q), pak můžeme maximální kinetickou energii elektronů Ek,max. přímo určit ze změřeného brzdného napětí U0 podle vztahu
| Ek,max. = e·U0 , | (4) |
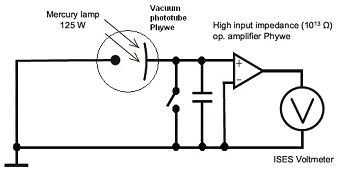
|
| Obr. 1: Schéma zapojení vakuové fotonky, k níž je paralelně připojený kondenzátor a spínač pro vybití. Fotokatoda je připojena ke kladnému vstupu operačního zesilovače, anoda k zápornému vstupu. |
Pomocí energetických úvah, konkrétně zákona zachování energie A. Einstein vysvětlil všechny pozorované vlastnosti vnějšího fotoefektu. Stačilo využít Planckův vztah pro energii Ef fotonu dopadajícího na fotokatodu
| Ef = h·f , | (5) |
- práci nezbytnou na vyražení elektronu ven z materiálu fotokatody – tzv. výstupní práci Wv
- a zbytek energie fotonu se přemění na kinetickou energii uvolněného elektronu ... Ek = e·U0.
Einsteinova rovnice pro vnější fotoefekt tedy vyjadřuje zákon zachování energie
| Ef = Wv + Ek , / −Wv | (6) |
| Ek = eU0 = Ef − Wv = h·f − h·fm . | (7) |
Vidíme, že záhadná mezní frekvence fm přímo souvisí s výstupní prací elektronu
| Wv = h·fm | (8) |
Einsteinovo vysvětlení fotoefektu na principu podobnosti, že pouze částice (foton) může interagovat s jinou částicí (zde elektron) dopomohlo k pozdější formulaci vlnově–částicové povahy světla, jež stojí na počátku zrodu kvantové mechaniky.
Nyní můžete pokračovat prostudováním návodu k experimentu pro zvolenou metodu.
B. Studium volt-ampérové charakteristiky vakuové fotonky
K prozkoumání vlastností vnějšího fotoelektrického jevu je vhodné použít vakuovou fotonku, ve které tudíž molekuly plynu neovlivňují tok elektronů od fotokatody k anodě. Můžeme snadno studovat, jak světlo dopadající na fotokatodu dokáže z jejího povrchu vyrazit a uvolnit elektron. Dokonce tok elektronů můžeme řídit přiloženým elektrickým napětím mezi anodou a fotokatodou – totiž záporné napětí na anodě (tzv. brzdné napětí) odpuzuje záporně nabité elektrony, které tedy až k anodě nemohou doletět. V takovém případě fotonkou neprochází žádný proud. Naopak kladné napětí na anodě elektrony přitahuje, odsává je od fotokatody a urychluje je směrem k anodě; pak můžeme naměřit větší hodnoty fotoproudu. Potenciální energie v elektrickém poli mezi anodou a fotokatodou (jež odpovídá práci elektrických sil působících na elektrony) se tak přeměňuje na kinetickou energii letících elektronů. Právě díky absolutní hodnotě brzdného napětí U0 máme možnost, metodu, jak tuto kinetickou energii Ek měřit.
kde e = 1,602.10−19 C je náboj elektronu v absolutní hodnotě. Pro kinetickou energii elektronů Ek se standardně používají dvě jednotky: joule (značka J, čti [džaul]) nebo elektronvolt (značka eV). Při udávání energie v elektronvoltech potom její číselná velikost přímo odpovídá velikosti brzdného napětí ve voltech.
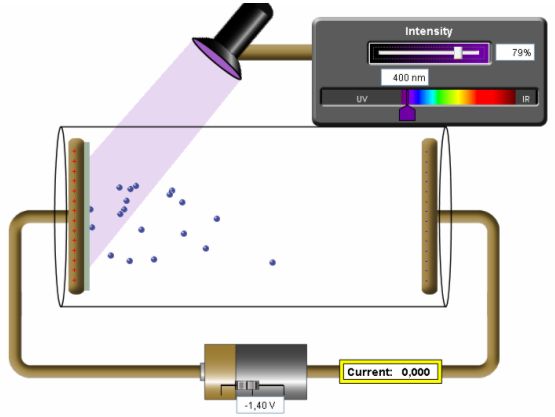
Obr. 1: Názorné vysvětlení vnějšího fotoefektu a měřicí metody při práci s apletem (http://PhET.colorado.edu). Elektrony uvolněné (vyražené) z fotokatody ultrafialovým světlem (400 nm) jsou zastaveny záporným, tzv. brzdným napětím (zde má brzdné napětí hodnotu −1,40 V) přivedeným na anodu, takže elektrony nemohou doletět až k anodě, a proto naměříme nulový proud.
Můžeme měnit napětí mezi anodou a fotokatodou prostřednictvím externího zdroje napětí a měřit hodnotu fotoproudu, tedy proměřit a zkoumat tzv. volt-ampérovou charakteristiku vakuové fotonky. Fyzikální vysvětlení i měřicí metoda přes brzdné napětí mohou být názorně demonstrovány a vysvětleny při použití apletu ‘Photoelectric effect’ (viz obr. 1) z projektu PhET. Aplet je volně dostupný na adrese
a vyžaduje jen nainstalované prostředí jazyku JAVA (JAVA Runtime Environment, JRE).
Je možné pozorovat hned několik zajímavých vlastností fotoproudu:
- Čím větší je intenzita světla dopadajícího na fotokatodu, tím větší fotoproud naměříme (podle očekávání).
- Velikost brzdného napětí, kdy je fotoproud nulový, resp. právě začíná narůstat, nezávisí na intenzitě světla (překvapivé s ohledem na klasické představy).
- Velikost brzdného napětí závisí jen na frekvenci dopadajího elektromagnetického záření. Dokonce byla pozorována velmi jednoduchá závislost (U0 = U0(f) = U0(1/λ), jejíž vysvětlení však bylo v začátcích problematické kvůli klasickým představám jevu – viz obr. 2a).
- Žádný fotoproud se neobjevuje, pokud je frekvence dopadajícího záření menší než určitá prahová frekvence f0 (tedy vlnová délka je větší než příslušná hodnota prahové vlnové délky λ0), která přímo souvisí s materiálem, z něhož je fotokatoda vyrobena.
- Je možné pozorovat saturaci fotoproudu pro vyšší velikosti brzdého napětí na anodě. Saturace fotoproudu je určena intenzitou dopadajícího elmg. záření. (Viz obr. 2b.)
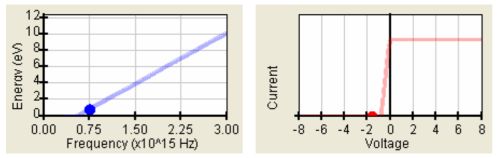
Obr. 2: a) jednoduchá závislost kinetická energie elektronů vs. frekvence dopadajícího elmg. záření, b) jednoduchá závislost v typických průbězích V-A charakteristiky s nulovým fotoproudem U < U0 a saturací fotoproudu (tzn. odkdy se fotoproud nemění pro větší kladná napětí).
Vlnová délka λ (resp. prahová vlnová délka λ0) odpovídá frekvenci f (resp. prahové frekvenci f0) přes vztahy
kde c = 3.108 m/s je rychlost světla ve vakuu. Pozorované vlastnosti II–IV byly obtížné k snadnému vysvětlení, ale experimentálně zjištěná závislost Ek(f) = eU0(f) byla jednoduše lineární funkce od frekvence f>f0
kde K je nějaký koeficient čili směrnice přímky (viz obr. 3).
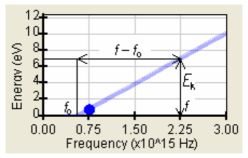
Obr. 3: Pozorovanou jednoduchou závislost kin. energie elektronů vs. frekvence záření lze snadno popsat lineární funkcí (3).
Všechny vlastnosti II–IV a experimentálně nalezená závislost (3) byly vysvětleny najednou Albertem Einsteinem v roce 1905, k čemuž A. Einstein využil dříve zformulovanou kvantovou hypotézu Maxe Plancka, že světlo se nešíří spojitě, ale po jakýchsi kvantech (tj. částicích, energetických balíčcích, r. 1926 nazvaných fotony), a to s energií Ephoton = hf, kde h = 6,63.10−34 J.s je Planckova konstanta. Proto pro K = h mohl A. Einstein pozorovanou závislost (3) interpretovat jako zákon zachování energie
tedy energie fotonů dopadajících na fotokatodu
se přemění jednak na výstupní práci W = h.f0 nezbytnou k vyražení (uvolnění) elektronů z fotokatody, jednak zbytek odpovídá kinetické energii Ek elektronů v okamžiku uvolnění. To znamená, že prahová frekvence záření přímo souvisí s výstupní prací a je určena materiálem fotokatody.
V tomto einsteinovském vysvětlení uvažujeme o interakci mezi dvěma částicemi (fotonu s dostatečnou energií a elektronu z fotokatody), nikoliv tedy mezi elektromagnetickým vlněním s částicí) a přitom zůstává splněn fundamentální zákon přírody – zákon zachování energie.
