Radioaktivita (5 experimentů)
Physical Background
Ve vzdálené úloze budeme zkoumat jednak zákonitosti statistiky, tzn. závislost naměřených hodnot na zvolené době, resp. počtu opakování měření, jednak závislost míry radiace na proměnlivých podmínkách, tj. na vzdálenosti od zdroje ionizujícího záření, na tloušťce vrstvy stínicího materiálu, příp. na druhu použitého stínicího materiálu. Míru radiace budeme vyjadřovat veličinou počet pulzů za určitý časový interval, kterou budeme měřit pomocí Geigerova-Müllerova detektoru.
Dílčí úlohy:
- Význam statistického zpracování – společný úvod ke všem dílčím úlohám.
- Přírodní pozadí – studium přirozeného radiačního pozadí (s možností ověřit platnost Poissonova rozdělení pro řídké jevy).
- Ochrana vzdáleností – základní intuitivní způsob ochrany před radiací společně s minimalizací doby expozice.
- Ochrana stíněním – standardní způsob ochrany před ionizujícím zářením využívaný v průmyslu i ve zdravotnictví.
I. Význam statistického zpracování
Statistika jako nástroj k popisu a předpovědím náhodného jevu
Pro náhodný neboli stochastický jev, kterým je např. radioaktivní přeměna nestabilního jádra a související vznik ionizujícího záření, nikdy nemůžeme předpovědět přesný okamžik, kdy nastane (např. narozdíl od budoucí polohy nějaké planety). Můžeme však měřit a předpovídat jakousi typickou míru výskytu, jinými slovy četnost pozorování při opakování jevu za delší časové období. Proto pro zvolenou délku tohoto časové intervalu má smysl měření několikrát zopakovat a naměřené hodnoty statisticky zpracovat:
Aritmetický průměr np – určuje hledanou míru radiace. Je to hodnota, kterou naměříme při větším počtu N opakování měření s největší pravděpodobností. Můžeme konstatovat, že existuje nějaká typická (průměrná, nejpravděpodobnější) hodnota, k níž se pro větší počet opakování měření bude zjištěný aritmetický průměr blížit. Nemůžeme však očekávat, že pro malé počty opakování měření tuto skutečnou hodnotu změříme přesně.
Standardní výběrová odchylka – určuje míru nejistoty, s jakou se námi naměřená průměrná hodnota odchyluje od neznámé skutečné hodnoty pro dané podmínky. Standardní výběrová odchylka má tedy význam přesnosti našeho měření za daných podmínek. S větším počtem opakování měření se přesnost měření bude zvyšovat, čili standardní výběrová odchylka (míra nejistoty) se bude zmenšovat.
A. Přírodní radiační pozadí – ověření Poissonova rozdělení
V první úloze budeme měřit hodnotu přírodního radiačního pozadí B, tzn. počet částic naměřený za určitý zvolený časový interval. Výsledkem bude aritmetický průměr Bp (z anglického background – pozadí) ze zvoleného počtu opakovaně měřených hodnot B a současně výběrová směrodatná odchylka σB jakožto chyba našeho měření. Naměřené pozadí zapíšeme ve tvaru
B = Bp ± σB (tzn. výsledek měření = střední hodnota ± chyba měření).
Důležitá poznámka pro ostatní úkoly
Při studiu fyzikálních zákonitostí platných pro ochranu před ionizujícím zářením nesmíme opomínat, že kromě zkoumané závislosti (na vzdálenosti od zdroje, na tloušťce materiálu) naměřená hodnota počtu pulzů zahrnuje i příspěvek přirozeného radiačního pozadí. Hodnotu pozadí můžeme měřit současně druhým GM čítačem a nesmíme ji zapomenout odečíst v každém měřeném bodě, nebo ji můžeme změřit zvlášť a odečíst průměrnou hodnotu pozadí od všech naměřených hodnot! (Oba postupy jsou správné.)
V ostatních úlohách tedy budeme zkoumat naměřený počet pulzů opravený o hodnotu přírodního pozadí v závislosti na vzdálenosti od zářiče či v závislosti na tloušťce vrstvy stínicího materiálu. Změříme několik bodů těchto závislostí. Přitom se můžeme přesvědčit o významu statistického zpracování a volbě počtu opakování měření (neboli závislosti na zvoleném rozsahu statistického souboru). Není vhodné použít jedinou naměřenou hodnotu pro každý bod zkoumaných závislostí. Měření v každém bodě závislosti bychom měli párkrát zopakovat a ve zpracování uvažovat průměrný počet pulzů a příslušnou výběrovou směrodatnou odchylku jakožto chybu měření v daném bodě. Zatímco jednotlivé naměřené hodnoty budou nejspíš značně rozptýlené kolem očekávané hladké závislosti, průměrné hodnoty budou rozptýlené méně a díky stanoveným chybám měření budou mít výsledky našeho experimentu lepší vypovídací hodnotu i spolehlivost. Navíc je možné stáhnout si data z dlouhodobého cyklicky opakovaného měření, vybrat ze souboru potřebné hodnoty a statisticky je zpracovat. Pro takto rozsáhlé výběrové statistické soubory budou průměry již prakticky tvořit hladkou křivku, s níž lze dobře srovnávat teoretickou závislost.
Ověření Poissonova rozdělení
Zájemci si pro zajímavost můžou ověřit zákon pro málo pravděpodobné jevy, který vystihuje tzv. Poissonovo rozdělení. Při opakování měření, které vždy trvá pevně určenou dobu (např. 1 minuta), naměříme různé hodnoty počtu pulzů Bi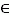 [0;Bmax], a to každou z těchto hodnot ni–krát. Tyto tzv. absolutní četnosti ni jsou úměrné pravděpodobnosti (nebo též relativní četnosti) pi naměření daného počtu pulzů (jinými slovy počet pulzů Bi naměříme s četností ni). Pro pravděpodobnosti pi=ni/Σni lze ověřit Poissonovo rozdělení, jež tyto konkrétní pravděpodobnosti řídkého jevu pi teoreticky předpovídá.
[0;Bmax], a to každou z těchto hodnot ni–krát. Tyto tzv. absolutní četnosti ni jsou úměrné pravděpodobnosti (nebo též relativní četnosti) pi naměření daného počtu pulzů (jinými slovy počet pulzů Bi naměříme s četností ni). Pro pravděpodobnosti pi=ni/Σni lze ověřit Poissonovo rozdělení, jež tyto konkrétní pravděpodobnosti řídkého jevu pi teoreticky předpovídá.
Například v kancelářském softwaru MS Excel můžeme využít statistické funkce PRŮMĚR, SMODCH a POISSON.
B. Ochrana vzdáleností od zdroje záření
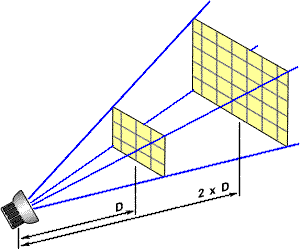
Ionizující záření stejně jako viditelné světlo a ostatní druhy záření musí splňovat základní závislost poklesu intenzity se vzdáleností od zdroje. Pro bodový zdroj klesá intenzita se čtvercem vzdálenosti, protože velikost sférické plochy v daném prostorovém úhlu roste s druhou mocninou (tedy se čtvercem) poloměru této sféry – viz obr. 1.
|
| Obr. 1: Ilustrace k zákonu převrácených čtverců – pokles intenzity záření s druhou mocninou vzdálenosti od zdroje záření. Jelikož účinná plocha detektoru (zde např. bližší žlutá ploška 3×4 políčka) se nemění a jelikož zářič vyzařuje do všech uvažovaných směrů stejně, v dvojnásobné (a dostatečně velké) vzdálenosti od zářiče naměříme čtyřikrát menší počet pulzů, protože příslušný prostorový úhel zde vymezený modrými přímkami bude čtyřikrát menší. |
V dostatečné vzdálenosti od zdroje můžeme zanedbat rozdíl mezi sférickou plochou a účinnou plochou detektoru. Rovněž i zdroj záření můžeme ve větších vzdálenostech považovat za bodový. Naopak poblíž zářiče je nezbytné uvážit přesnou geometrii pokusu a závislost se stává složitější.
C. Ochrana vrstvou stínicího materiálu
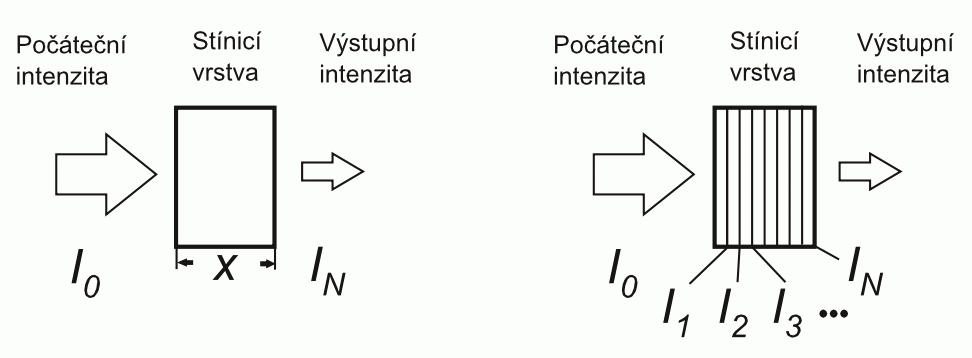
Prochází-li ionizující záření vrstvou hustšího materiálu, nějaká část vstupní intenzity I0 může být v materiálu pohlcena (absorbována) a tedy neprojde dále za překážku. Za bariérou tedy naměříme sníženou intenzitu záření, resp. míru radiace, tzn. nižší počet pulzů za zvolený časový interval. Chceme-li najít teoretickou závislost poklesu počtu pulzů na tloušťce vrstvy, rozdělme si celý materiál na více mezivrstev o stejné tloušťce i dalších vlastnostech. Můžeme předpokládat, že každá mezivrstva zeslabí vstupní intenzitu stejnou měrou, tedy že skrze každou mezivrstvu projde vždy stejná procentuální část β = I1/I0 = I2/I1 = I3/I2 = … = IN/IN−1 < 1 (viz obr. 2). Proto platí
| I1 = β I0 , I2 = β I1 = β·β·I0 = β2I0 , I3 = β I2 = β3I0 , … IN = β IN − 1 = βNI0 . | (1) |
|
| Obr. 2: Odvození Lambertova–Beerova zákona. |
Poměr β je závislý na materiálu a zejména na volbě tloušťky uvažovaných mezivrstev. Chceme-li tento parametr nahradit vhodnou materiálovou charakteristikou, která standardně uvažuje zeslabení e-krát (kde Eulerovo číslo e = 2,71828… je základem přirozené exponenciální funkce), pak můžeme počet mezivrstev N považovat za přímo úměrný celkové tloušťce stínicí vrstvy x, tzn. N = k·x. Po dosazení do výše uvedeného vztahu a elementárních úpravách (β = eln β) dostáváme pro měřenou zeslabenou intenzitu
| IN = βNI0 = (eln β)NI0 = (eln β)kxI0 = I0 eln β kx = I0 e−Cx , | (1) |
Odvodili jsme tak závislost počtu pulzů (N(x) − B) ionizujícího záření (tj. po odečtení přírodního pozadí B), který za určitou dobu naměříme za vrstvou stínicího materiálu tloušťky x, na této tloušťce. Pokles této funkce je typicky exponenciální.
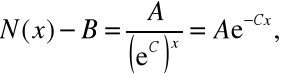
| (1) |
Polovrstva [mm]
| E [keV] | voda | beton | železo | olovo |
|---|---|---|---|---|
| 200 | 51 | 21 | 6,6 | 1,4 |
| 500 | 78 | 30 | 11,1 | 4,2 |
| 1000 | 102 | 45 | 15,6 | 9 |
| 2000 | 144 | 59 | 21 | 13,5 |
| 5000 | 231 | 99 | 28,8 | 14,7 |
| Tab. 1: Tabulka polovrstev vody, betonu, železa a olova pro různé energie gama záření (převzato z Ullmann V.: Jaderná fyzika a fyzika ionizujícího záření). |
