Spektra
Physical Background
Označení kvantová fyzika předpokládá, že základní veličiny popisující objekty v mikrosvětě (např. elementární částice) nemohou nabývat libovolných hodnot, jak jsme zvyklí v případě objektů makrosvěta, ale jen určitých dovolených hodnot. V úvodu jsme zmínili kvantování energie elektronu v atomovém obalu. Obdobně se kvantování týká i momentu hybnosti elektronu, u něhož si představujeme, že obíhá kolem jádra atomu, a podobně i dalších fyzikálních veličin.
Těmito úvahami, které vypadaly poněkud uměle, již v roce 1913 Niels Bohr odvodil výraz pro energii a moment hybnosti elektronu v atomu vodíku.
Proč jsou základní veličiny kvantovány, nám může pomoci objasnit pravděpodobnostní interpretace vlnové funkce. Vlnová funkce je základní prostředek pro popis vlastností objektů v mikrosvětě. Samotnou vlnovou funkci si těžko spojíme s nějakou názornou představou – mimo jiné proto, že její funkční hodnoty musí být komplexní čísla, nicméně kvadrát absolutní hodnoty vlnové funkce (což je vždy reálné číslo) je úměrný pravděpodobnosti naměření určité dovolené hodnoty fyzikální veličiny (např. polohy, hybnosti, energie, …). V jednoduchých systémech, kterým je rovněž atom vodíku, by se míra pravděpodobnosti v prostoru neměla měnit skokově, ale plynule, spojitě!
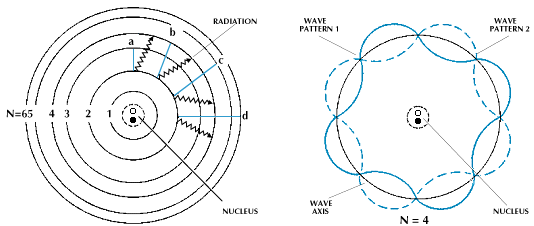
Spojitý průběh vlnové funkce může mít pouze takový elektron, který se nachází na energetické hladině ve vzdálenosti r od jádra, kam se vejde celočíselný násobek vlnových délek. Použijeme-li pro vlnovou délku λB objektu mikrosvěta de Broglieho vztah
![]() ,
,
potom můžeme kvantovací podmínku vyjádřit rovnicí
|
| (1) |
kde 2πr je délka dráhy (tj. obvod kružnice o poloměru r), h = 6,63·10−34 J·s je Planckova konstanta, m je hmotnost a v velikost rychlosti pohybu mikroobjektu a konečně n je přirozené číslo (celočíselný násobek), kterému říkáme hlavní kvantové číslo. Z rovnice (1) po vynásobení mv/(2π) pro moment hybnosti L = rp = rmv plyne kvantovací podmínka
|
| (1a) |
a speciálně pro oběžnou rychlost
|
| (1b) |
resp. pro její kvadrát
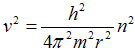 . .
| (1c) |
Oběžná rychlost v a poloměr orbity r vzájemně souvisejí přes
silové působení. Coulombovská přitažlivá síla 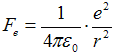 mezi elektronem a protonem o velikosti
náboje e = 1,602·10−19 C způsobuje dostředivé zrychlení
mezi elektronem a protonem o velikosti
náboje e = 1,602·10−19 C způsobuje dostředivé zrychlení 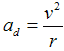 , proto dále platí
rovnice
, proto dále platí
rovnice
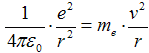 ,
/ . r ,
/ . r
| (2) |
kde me = 9,1·10−31 kg je hmotnost elektronu. Odsud dostáváme pro kinetickou energii
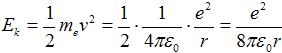 . .
| (2a) |
Dosazením kvantovací podmínky (1c) za kvadrát oběžné rychlosti v2 do rovnice (2) obdržíme
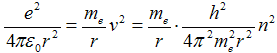 , ,
|
odkud po úpravách dostaneme kvantovací podmínku pro poloměr oběžné dráhy elektronu kolem jádra atomu
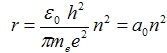 , ,
| (2b) |
kde 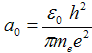 = 5,29·10−11 m označuje tzv. Bohrův poloměr pro základní orbitu elektronu v atomu vodíku.
= 5,29·10−11 m označuje tzv. Bohrův poloměr pro základní orbitu elektronu v atomu vodíku.
Uvážíme-li, že potenciální energie při volbě nulové hladiny v nekonečnu je nepřímo úměrná první mocnině vzdálenosti podle vztahu
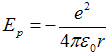 , ,
|
potom pro celkovou energii s dosazením (2a) platí
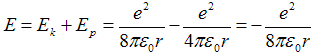 . .
|
A konečně po dosazení (2b) za poloměr r je energie elektronu v atomu vodíku kvantována podle vztahu
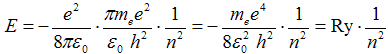 , ,
| (3) |
kde základní energie elektronu v atomu vodíku se označuje jeden rydberg a má velikost
1 Ry = −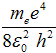 = −13,6 eV . = −13,6 eV .
|
Vznik čárových spekter pak můžeme jednoduše vysvětlit přeskoky elektronu mezi dovolenými hladinami energie, které označíme hlavními kvantovými čísly m a n (m > n, tzn. En > Em). Při přeskoku elektronu z vyšší energetické hladiny na nižší je z důvodu zákona zachování energie vyzářen foton o energii odpovídající právě rozdílu energií mezi uvažovanými hladinami
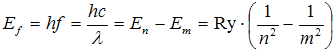 . .
| (4) |
Odtud dostáváme vztah pro vlnovou délku spektrální čáry na základě tzv. Ritzova–Rydbergova kombinačního principu
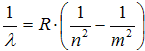 , ,
| (5) |
kde ![]() 1,0974·107 m−1 značí tzv. Rydbergovu konstantu.
1,0974·107 m−1 značí tzv. Rydbergovu konstantu.
Pro vlnové délky tzv. Balmerovy série spektrálních čar vodíku (týká se seskoků elektronů zpět na druhou hladinu, n = 2, m > 2) platí formule (5) přesně. Dále z teorie plyne, že čím menší je energetický rozdíl mezi hladinami, tím pravděpodobnější je příslušný přeskok elektronu a vyzáření (emise) fotonu. Proto přeskoky mezi sousedními hladinami způsobují nejjasnější emisní čáry ve spektru a v rámci dané série pak intenzita čar postupně klesá!
| Tyto stránky a vzdálené experimenty vznikly v rámci projektu č. 957/2012 Výuka kvantové fyziky metodou integrovaného e-learningu, financovaného Fondem rozvoje vysokých škol (www.frvs.cz). |
