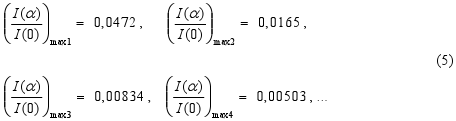Гибка света на щели
Physical Background
To explain the diffraction phenomenon, we will use Fraunhofer´s theory. This theory assumes, that a wave that falls on a slit is planar (Fig. 1). Diffraction phenomena of this type are called Fraunhofer´s diffraction and we will explain it on the basis of the elementary concepts in Fig. 1 and Fig. 2.
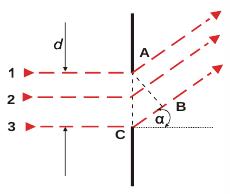
Figure 1 The Fraunhofer’s diffraction phenomenon on a slit.
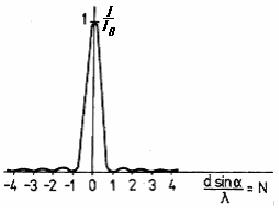
Figure 2 The distribution of the light intensity behind the slit and the condition for the location of minima
We assume that a planar monochromatic and coherent wave falls on the single slit of the width d = |AC|, and diffracts at an angle α, defining randomly chosen direction (see Fig.1). If the distance |BC| is just equal to the wavelength λ, then the sum of intensities of electric field from all the rays (of electromagnetic radiation ) that emerge from the slit in this direction is zero, or all these rays cancel in this direction. It may be proven by a simple logic: to every ray falling in the interval between the rays 1 and 2 corresponds only one ray from the other half of the slit, 2 and 3, which . mutually differ from each other a difference λ/2, and so they cancel each other Therefore, if we consider that a relation |BC| = d.sin α is valid and admit also another nonzero integer multiple of wavelength λ, we get a condition for the location of all minimum values ( see Fig. 2). The exact derivation of the diffraction pattern (which is not needed for a student ) derived by Fraunhofer, gives the detailed distribution of the intensity with the main maximum and number of other maxima and minima ( Fig . 2 ). This intensity can be expressed as a function of an angle α

-
The location of minima of intensity (i.e. I(α) / I(0) = 0 ) in directions where it is
or the condition for the angles αmin,
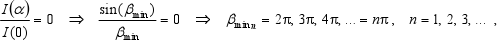
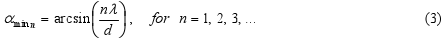
-
The location of maxima of intensity (i.e. I(α)/I(0) = max.) is then in points, where it is
or the condition for angles αmax
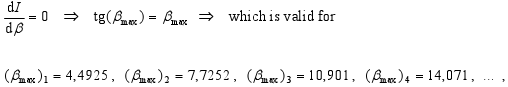
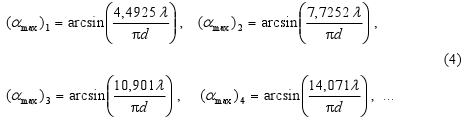
-
The relative magnitude of maxima of intensity (i.e. I(α) / I(0) ) in points where it is