Ohyb elektromagnetického žiarenia
Physical Background
Ohybové javy, ktoré vznikajú v tesnej blízkosti prekážky pri prechode svetla z bodového zdroja podrobne skúmal Fresnel. Pri týchto javoch, ktoré nazývame Fresnelove ohybové javy, ide o problém riešenia interferencie guľových vĺn na základe Huygensovho princípu. Ak však uvažujeme ohyb svetla z dosť vzdialeného zdroja (monochromatického koherentného žiarenie), vlnoplocha je prakticky už rovinná. Tým sa dostávame k javom, ktoré nastávajú pri ohybe zväzku rovnobežných lúčov s presne rovinnými vlnoplochami, a ktoré sa nazývajú Fraunhoferove ohybové javy.
Keďže sme v experimente v dostatočnej vzdialenosti od zdroja kvalitatívnu i kvantitatívnu analýzu nám podáva Fraunhoferov ohybový jav – v našom prípade na jednorozmernej štrbine. Štrbina AC šírky d osvetlená kolmo dopadajúcim monochromatickým svetlom (jednofarebným svetlom, t.j. svetlom s jednou vlnovou dĺžkou) sa stáva v každom svojom bode v celej jej šírke zdrojom elementárnych vĺn (podobne ako rozhranie medzi dvomi prostrediami pri lome a odraze). Zo všetkých bodoch sa šíria guľové vlnoplochy. Pretože však lúče vystupujúce všetkými smermi medzi sebou interferujú, nešíri sa svetlo za štrbinou rovnomerne na všetky strany, ako pozorované rozdelenie intenzity v experimente ukazuje.
Vyberme si zo všetkých lúčov rovnobežný zväzok lúčov vystupujúcich zo štrbiny pod uhlom α (odklon od pôvodného smeru lúčov pred dopadom na štrbinu, pozri obr. 1).
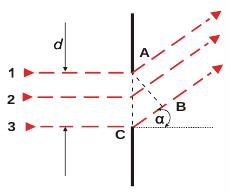
Obr. 1 K teórii Fraunhoferoveho ohybového javu na štrbine
V rovinnej vlnoploche AB, kolmej na smer šírenia sa vlnenia, majú jednotlivé zväzky rôznu fázu, podľa dĺžky prebehnutej dráhy. Ak je napr. δ oneskorenie krajného lúča CB vzhľadom na druhý krajný lúč v bode A (lúč 1), je oneskorenie lúča, ktoré prechádza stredom štrbiny (t.j. osového lúča) polovičné, teda δ/2. Fázový rozdiel všetkých ostatných lúčov rastie úmerne so vzdialenosťou lúčov od bodu A k bodu C. Teda ku každému lúču p (nachádzajúceho sa medzi lúčmi 1 a 2) nájdeme medzi lúčom 2 a 3 taký lúč p´, ktorý bude vzdialený o pol šírky štrbiny) a teda bude mať dráhový rozdiel δ/2. Z tohto môžeme usudzovať, že všetky lúče sa budú rušiť ak, ich oneskorenie je rovné nepárnemu počtu polovĺn, teda ak bude odchýlka lúčov taká, že sa δ rovná párnemu počtu polovĺn a teda celočíselnému násobku vĺn, čo vyjadruje rovnica:
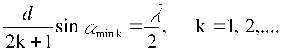
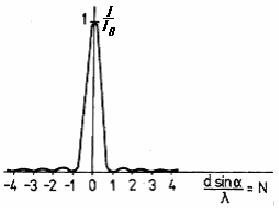
Obr. 2 Rozloženie intenzity žiarenia po prechode štrbinou šírky d
Vysvetlenie ohybového javu pre potreby laboratórnej úlohy urobíme len na základe elementárnych predstáv z obr. 1 a použijeme teóriu, v ktorej sa predpokladá, že dopadajúca vlna na štrbinu je rovinná (obr. 1), t.j. jedná sa Fraunhoferov ohybový jav.
Predpokladajme, že rovinná monochromatická a koherentná vlna dopadá na jedinú štrbinu šírky d = |AC| a odchyľuje (ohýba) sa od pôvodného smeru sa o uhol α definujúci náhodne vybraný smer (pozri obr. 1). Ak by sa vzdialenosť |BC| rovnala práve vlnovej dĺžkeλ, potom možno z úsudku ľahko zistiť, že súčet intenzít elektrického poľa od všetkých lúčov (elektromagnetického žiarenia), ktoré zo štrbiny vystupujú v tomto smere, je nulový, inými slovami sa tieto lúče navzájom vyrušia. Každému lúču medzi lúčmi 1 a 2 odpovedá totiž lúč z druhej polovice štrbiny 2 až 3, ktorý sa od neho líši práve o dráhový rozdiel λ/2, takže sa s ním v dôsledku interferencie ruší (takúto dvojicu predstavujú napr. lúče 1 a 2, pričom lúče 1 a 3 sú limitne blízko k okraju štrbiny a jeden z nich – nevykompenzovaný, nehrá úlohu). Preto, ak zvážime platnosť vzťahu |BC| = d.sin α a pripustíme ľubovoľný nenulový celočíselný násobok vlnovej dĺžky λ, dostaneme úvahou podmienku pre polohu miním (3). Exaktným riešením (napr. [1]) ohybového javu, ktoré však nie je pre potreby praktika nevyhnutné, Frauenhofer získal rozloženie intenzity prechádzajúceho žiarenia s hlavným maximom a symetricky s vedľajšími maximami a minimami (obr. 2). Intenzitu žiarenia po prechode štrbinou možno vyjadriť ako funkciu uhla α:

-
Poloha miním intenzity (t.j. I(α) / I(0) = 0 ) je v smeroch, kde je splnená podmienka:
resp. podmienka pre uhly αmin, pre ktoré nastáva minimum, je:
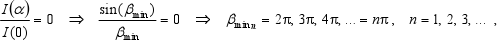
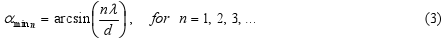
-
Poloha maxím intenzity (t.j. I(α)/I(0) = max.) je potom v miestach, kde je splnená podmienka:
alebo podmienka pre uhly αmax, pri ktorých nastáva maximum, je:
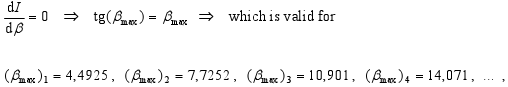
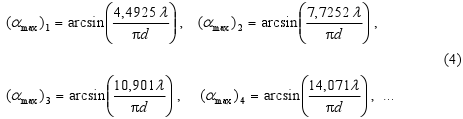
-
Relatívna veľkosť maxím intenzity (t.j. I(α) / I(0) ) v miestach, kde je splnená podmienka (4), je: