Heisenbergov princíp neurčitosti
Physical Background
Heisenbergov princíp neurčitosti postuluje, že lokalizácia stavu a hybnosti ľubovoľnej častice nemôže byť súčasne s nekonečnou presnosťou. Uvažujem fotón hmotnosti m a hybnosti p. Ak meriame polohu fotónu s neurčitosťou Δy a súčasne jeho hybnosť v smere pohybu fotónu s neurčitosťou Δpy, potom podľa Heisenbergovho princípu by malo platiť

Urobme verifikáciu Heisenbergovho princípu pomocou fotónu obsiahnutého v lúči svetla vychádzajúceho z laseru, ktorý prechádza štrbinou šírky d kolmo na rovinu štrbiny a tiež kolmo na tienidlo nachádzajúce sa vo vzdialenosti a od štrbiny (obr. 1). V nami uvažovanom prípade vektor hybnosti fotónu p má zložky px= mc a py = 0, kde m je hmotnosť fotónu a c = 3,00·108 ms-1 je rýchlosť svetla (obr. 2).
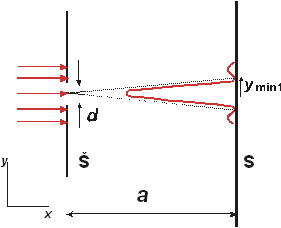
Obr.1 Geometria experimentu difrakcia na šrbine (Š – štrbina, S – tienidlo)
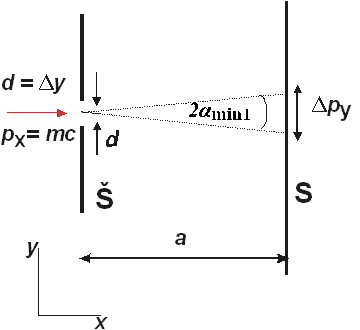
Obr. 2 Hybnosť fotónu pri ohybe na štrbine (Š – štrbina, S – tienidlo)
Prechod fotónu cez štrbinu šírky d je vlastne meranie jeho polohy v smere osi y, s výsledkom určenia polohy y s neurčitosťou Δy = d. Čo je skutočne pravda, pretože fotóny, ktoré preleteli štrbinou a nachádzajú sa už za ňou na tienidle, mali by mať v určitom okamžiku polohu y ± d/2. Preto môžeme napísať pre neurčitosť polohy fotónu
Skúmajme vektor hybnosti p fotónu za štrbinou. Kým fotón pred štrbinou, pohybujúci sa kolmo smerom na štrbinu má zložky vektora hybnosti px = mc, py = 0, t.j.. len v smere osi x (obr. 2), fotón za štrbinou má aj zložku hybnosti v smere osi y, ktorú označíme py. Dostaneme polohu prvého minima vzhľadom na polohu hlavného difrakčného maxima ako neurčitosť momentu hybnosti fotónu v smere y-osi (obr. 2)
Aká je veľkosť odpovedajúceho uhla αmin1? Fotón je častica s hmotnosťou m a hybnosťou p. Z vlnových vlastností fotónu na základe de Broglieho vzťahu pre vlnovú dĺžku vyplýva, že vlnová dĺžka λ je nepriamo úmerná veľkosti vektora hybnosti p

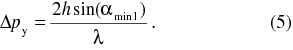
Na základe geometrie z obr. 2 platí
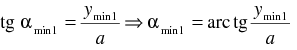
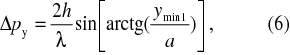
Ak vynásobíme neurčitosti v rovnici (2) a (6) a predpokladáme platnosť Heisenbergovho princípu neurčitosti, formulovaného vzťahom (1), dostávame nerovnosť
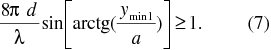
Na základe našich meraní, daných hodnôt a pomocou vzťahov (2) pre Δy a (6) pre Δpy , s následným využitím vzťahu (1), možno nájsť približnú hodnotu h, hodnotu jednej zo základných fyzikálnych konštánt h – Planckovej konštanty, ktorá potvrdzuje platnosť Heisenbergovho princípu neurčitosti.
