Vlastné a vynútené kmity
Physical Background
Harmonický oscilátor
Teleso vykonávajúce harmonický kmitavý pohyb nazývame harmonický oscilátor. Môže ním byť v prvom priblížení napríklad teleso na pružine (obr. 1), alebo atóm či molekula pevnej látky. Ak pri jeho pohybe zanedbáme odpor prostredia, hovoríme o netlmenom harmonickom oscilátore. Môžeme ukázať, že kmitanie je vždy harmonické, ak je pôsobiaca sila úmerná výchylke z rovnovážnej polohy. A body making an oscillatory harmonic motion is called the harmonic oscillator. At the first approximation it may be e.g. a body suspended on a spring (Fig. 1) or an atom or a molecule of a solid.
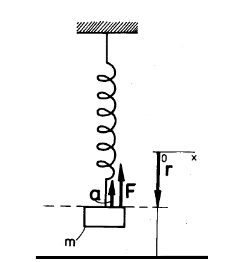
Obr. 1 Schematické reprezentácia harmonického oscilátora, F - elastická sila, r – výchylka, a - zrýchlenie
Majme pružinu, na ktorej natiahnutie o r je potrebná sila F = -kr, kde k je tuhosť pružiny. Pohybová rovnica harmonického oscilátora, ktorý je tvorený touto pružinou a závažím hmotnosti m, je (ako aplikácia druhého Newtonovho zákona ΣF = ma):


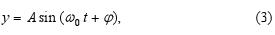
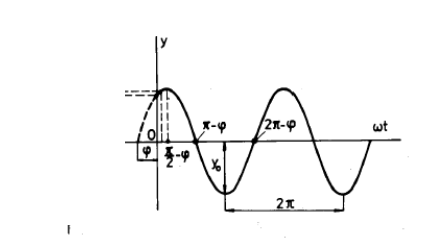
Obr. 2 Grafické vyjadrenie pohybu harmonického oscilátora
Pre vlastnú uhlovú rýchlosť harmonického oscilátora môžeme napísať:
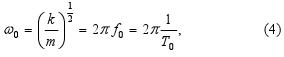
Tlmený oscilátor
Pri pohybe harmonického oscilátora v reálnych podmienkach pôsobia vždy trecie sily, ktoré amplitúdu kmitavého pohybu zmenšujú a po určitom čase kmitanie prestane. Taký oscilátor nazývame tlmený oscilátor.
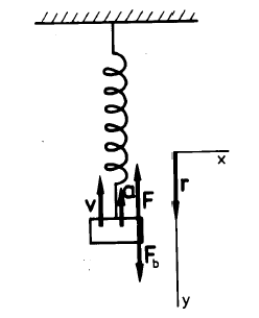
Obr. 3 Tlmený oscilátor a) F je elastická sila, Fb je brzdná sila, r je výchylka, v je okamžitá rýchlosť a a je okamžité zrýchlenie, b) s tlmením v dôsledku trenia v kvapaline
Trecia sila je pri malých rýchlostiach priamo úmerná okamžitej rýchlosti telesa v hmotnosti m:
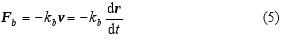

Zaveďme veličinu b = kb/(2m), ktorá sa nazýva konštanta útlmu, [b] = s−1. Pre malé tlmenie (b < ωo) má rovnica (6) riešenie, (ak si uvedomíme, že podľa obr. 3 platí r = jy):
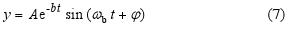
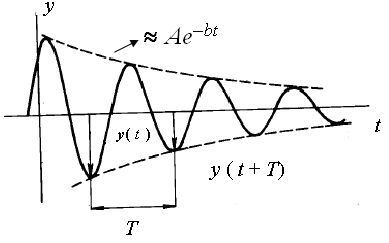
Obr. 4 Grafické vyjadrenie časovej závislosti výchylky tlmeného oscilátora
Vynútené kmity oscilátora
Významným prípadom kmitavého pohybu je takzvané vynútené kmitanie, pri ktorom vonkajšia sila núti látkový objekt kmitať s všeobecne iným kmitočtom ako je kmitočet vlastných kmitov. Ak sa však oba kmitočty k sebe približujú, vzniká dôležitý jav, ktorý nazývame rezonancia. Predpokladajme, že na závažie z obr. 1 pôsobí vynucujúca periodická sila:

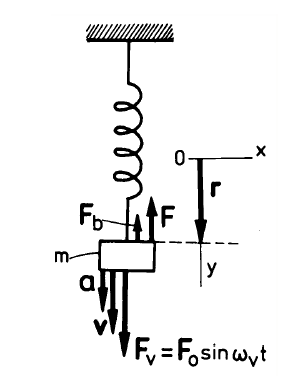
Obr. 5 Tlmený oscilátor s pôsobiacimi silami: Fv - vynucujúca sila, F - elastická sila, Fb - brzdná sila, r je okamžitá výchylka, v okamžitá rýchlosť a a je okamžité zrýchlenie telesa hmotnosti m.
Ak zvážime všetky sily, ktoré spôsobujú pohyb závažia, môžeme napísať pohybovú rovnicu pre pohyb v osi y: If all the forces that make the weight to move are considered, the following equation of the motion may be written
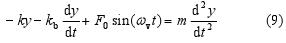
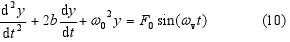

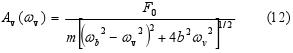
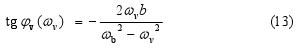
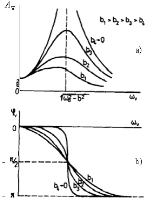
Obr. 6 Grafický priebeh: a) amplitúdy vynútených kmitov Av s koeficientom tlmenia b ako parameter, b) fázy vynútených kmitov φv, v závislosti na uhlovej frekvencii ωv vynucujúcej sily
Z grafov na obr. 6 vyplýva množstvo zaujímavých poznatkov pre vynútený harmonický pohyb. Po prvé, je zrejmé, že amplitúda vynútených kmitov Av (pozri obr. 6 a) je funkciou uhlovej frekvencie ωv vynucujúcej sily. Maximum amplitúdy pre vynútený harmonický pohyb nastáva pre takzvanú rezonančnú frekvenciu:

Závislosti na obr. 6 možno využiť na určenie prenosu energie na oscilátor. Tento proces je veľmi dôležitý v prírode a vo všeobecnosti v technológiách, pretože reprezentuje selektívny prenos energie medzi vysielačom energie a oscilátorom len v istých intervaloch frekvencií, resp. vlnových dĺžok. Tento jav tvorí napr. základ selektívneho prenosu telekomunikačných signálov, alebo absorpcie určitých vlnových dĺžok žiarenia zo Slnka určitými molekulami, ktoré, mimo iného, dosiahnu povrch Zeme.
Prenos energie za jednotku času na oscilátor (alebo okamžitý výkon Pv, ktorý je funkciou času) z vynucujúceho zdroja je:
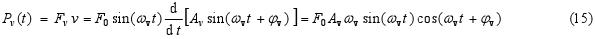
Stredná hodnota energie prenesená za jednu periódu harmonického pohybu oscilátora zo zdroja vynucujúcej sily na oscilátor závisí od uhlovej frekvencie vynucujúcej sily ωv. Viac informácii možno nájsť v práci R. B. Lindsay, Physical Mechanics, 3rd ed., Van Nostrand 1962).
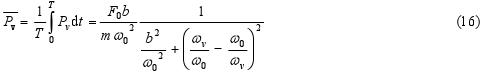
Obr. 7 prezentuje prenos strednej hodnoty energie počas jednej periódy harmonického pohybu na oscilátor zo zdroja vynucujúcej sily ako funkciu uhlovej frekvencie ωv, pre dve rôzne hodnoty tlmenia b.
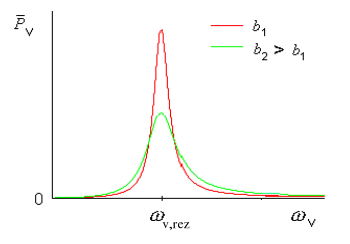
Obr. 7 Závislosť preneseného stredného výkonu počas jednej periódy pohybu harmonického oscilátora (pre dve rôzne hodnoty tlmenia b).
